O novo mulligan em números

1. INTRODUÇÃO

Este artigo começa com uma história triste. No mesmo dia em que pensei em escrevê-lo, e comecei a fazer algumas contas, o matemático Frank Karsten publicou na página da Channelfireball um artigo, aliás excelente, com teor muito similar. O trabalho dele é mais profundo que este então, se você tem facilidade com o Inglês, recomendo muito a leitura do artigo de Frank Karsten sobre o assunto.

No artigo citado, a matemática subjacente não é mostrada, são apresentados apenas resultados finais e conclusões. Por outro lado, há vários artigos pela rede que discutem os princípios de análise combinatória necessários já contextualizados no Magic. Eu recomendo dois, infelizmente escritos em língua inglesa, sendo um deles um artigo mais antigo do próprio Frank Karsten, uma introdução à distribuição hypergeométrica para jogadores de magic, e outro do Chris Mascioli sobre matemática e a distribuição geométrica.

A conclusão da história triste seria a desistência em apresentar meus modestos cálculos para a Cards Realm. Detestaria dar a impressão de que plagiei a ideia de alguém, o que absolutamente não é verdadeiro, fui apenas traído por um timing azarado. Voltei atrás por dois motivos. O primeiro é o fato de que estes artigos estão em inglês e pensei que o texto em português poderia ser útil a alguém. O segundo é meu gosto pessoal pelos meandros da matemática agregada ao tema, além da apresentação dos resultados finais num formato um pouco diferente e, na minha opinião, de consulta mais fácil. Afinal, matemática é vida, matemática é amor.

O objetivo central deste texto é apresentar aos colegas jogadores, que eventualmente não conheçam, o princípio matemático básico que rege o Magic, ou qualquer jogo de cartas, conhecido como Distribuição Hipergeométrica. Conhecê-la é extremamente útil para deckbuilding, especialmente nos momentos em que você se pergunta quantas cópias de uma determinada carta deve incluir na sua lista. Em seguida, proponho que apliquemos esta ferramenta a uma questão que vem causando apreensão a todos nós desde o dia 26 de fevereiro deste ano: a possível substituição do mulligan de Vancouver pelo mulligan de Londres a partir do próximo Mythic Championship (ProTour). O problema que nos acompanhará até o final do artigo é como determinar a probabilidade de ter ao menos uma cópia de alguma carta específica na mão inicial e como essa probabilidade se comporta com a mudança de regras. Olá, Leylines, estou olhando pra vocês.

Não entre em pânico! A matemática é universal, mas o amor por ela não. Sei disso. Se por acaso você faz parte do nobre grupo de pessoas que vê o assunto como uma chateação gigante, não precisa parar de ler ainda. Calma. Respire fundo e pule as seções 2 e 5, porque as contas de verdade estão restritas a elas, e aí vá direto ao que interessa. Juro que não fico nem um pouco chateado. Se serve de estímulo, te garanto que a discussão matemática é viável para quem quer que tenha concluído o Ensino Médio. Se é aprazível ou não é que depende do gosto do freguês.

2. A DISTRIBUIÇÃO HIPERGEOMÉTRICA

Quantas mãos iniciais de 7 cartas são possíveis?

Para responder a esta primeira pergunta, basta utilizar combinações. Precisamos calcular o número de combinações de n elementos retirados em grupos de k elementos, ou seja, o número de mãos de k cartas (No nosso caso, k=7) retiradas aleatoriamente, sem reposição e sem considerar a ordem, de um conjunto de n cartas (No nosso caso, n=60). O cálculo faz uso do fatorial, representado pelo ponto de exclamação. Para quem não se lembra, o fatorial de um número inteiro é o produto deste número por todos os inteiros abaixo dele até 1 (Ex: 3!=3x2x1=6).

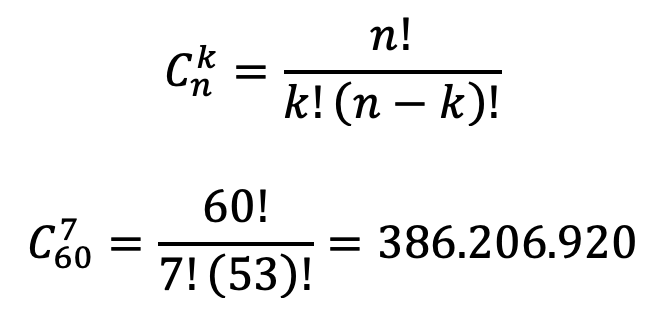
Temos então um total de aproximadamente 386 milhões de mãos iniciais de 7 cartas possíveis numa partida de Magic. Note, no entanto, que estas mãos iniciais não são todas únicas, já que nossos decks possuem degenerescências, ou seja, cartas em múltiplos.

Quantas mãos iniciais de 7 cartas contem exatamente uma cópia de uma certa carta?

Digamos que o deck de n cartas (n=60) contenha m cópias da carta em questão (m=4 por hora) e que gostaríamos de ter exatamente x delas (x=1) na mão inicial de k cartas (k=7 por hora). Fazemos uso então do princípio fundamental da contagem: o número total de mãos iniciais desejáveis é o número de combinações de m cartas retiradas em grupos de x (o sucesso em ter x cópias da carta) MULTIPLICADO pelo número de possibilidades sem a carta desejada, correspondendo às demais cartas da mão, ou seja, a combinação de n-m cartas retiradas em grupos de k-x. Isto é, uma carta entre 4 e quaisquer 6 entre as outras 56:

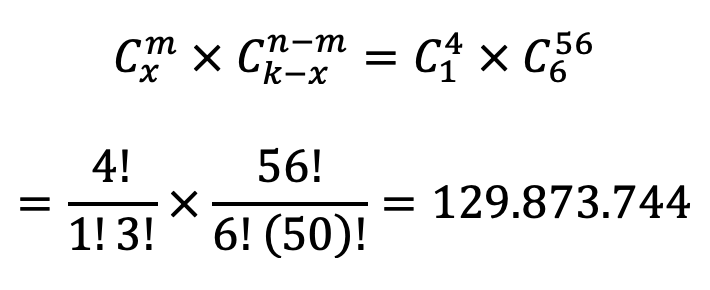
Temos então um total próximo de 130 milhões de mãos iniciais que contém exatamente uma cópia de uma carta específica de um total de 4 cópias.

- Qual é a probabilidade de que a mão inicial contenha exatamente uma cópia de uma certa carta?

Para saber a probabilidade de que algo ocorra, basta dividir o número de casos favoráveis pelo número total de casos. No exemplo em questão, basta dividir, um pelo outro, os dois números já calculados:

P(1) = 129.873.744/386.206.920 = 0,336 = 33,6%.

A forma geral deste cálculo é o que conhecemos como Distribuição Hipergeométrica, que pode ser sintetizada assim:

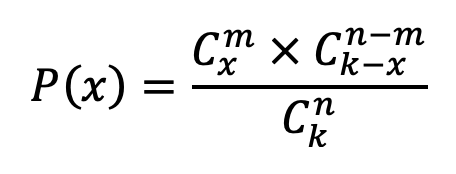
Qual a probabilidade de que a mão inicial contenha ao menos uma cópia de uma certa carta?

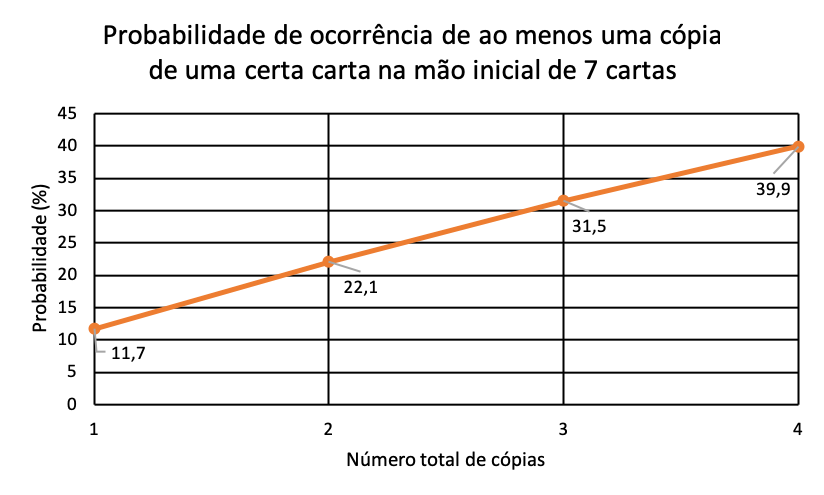
Os cálculos até aqui consideraram apenas a probabilidade de que a mão inicial contenha exatamente uma cópia da carta. Entretanto, se você quer muito aquela carta, deve aceitar mãos que contenham mais do que uma cópia. Precisamos, portanto, computar a probabilidade acumulada, ou seja, considerar também os casos em que você abre com 2, 3 ou 4 cópias dela (supondo que o total seja 4). A correção a fazer aqui, embora trabalhosa, é simples: basta refazer os cálculos com x=2, x=3 e x=4 e somar todos os resultados com o que já temos para x=1. O mesmo raciocínio vale se você quer uma ou duas cópias, mas não aceita três ou quatro, por exemplo. Basta somar as probabilidades dos casos de interesse. A probabilidade de termos ao menos uma cópia (aceitando até 4) aumenta de 33,6% para 39,9% aproximadamente.

A título de curiosidade, você poderia refazer os cálculos considerando que tem três, duas ou apenas uma cópia da tal carta no total, bastando mudar o valor de m. O resultado é o seguinte:

3. FERRAMENTAS COMPUTACIONAIS

Se você está familiarizado com o uso do Excel, vai encontrar todas as funções relevantes (fatoriais, combinações e a própria distribuição hipergeométrica) embutidas no pacote, mas há uma forma bem mais simples e direta de fazer cálculos de probabilidade acerca de decks de Magic. Existem calculadoras online bastante práticas espalhadas pela rede. A mais popular delas, que recomendo e usarei deste ponto em diante, está no site Stat Trek, que você encontra aqui.

Como ilustração do uso da calculadora hipergeométrica, vamos refazer o cálculo da seção anterior: qual a probabilidade de que tenhamos uma determinada carta, de um total de 4, na mão inicial de 7 cartas num deck de 60?

Note que a calculadora fornece as probabilidades acumuladas diretamente, o que é extremamente útil. P(x=1) é a probabilidade de que tenhamos exatamente uma cópia da carta (é o 33,6% que encontramos na seção anterior), P(x<1) é a probabilidade de fracasso, ou seja, nenhuma cópia da carta, P(x>1) é a probabilidade de que tenhamos mais do que uma cópia e P(x>=1) a probabilidade de que tenhamos uma ou mais cópias (é o 39,9% citado na seção anterior).

4. A MUDANÇA DA REGRA DE MULLIGAN

É provável que o leitor conheça bem o mulligan atual, denominado mulligan de Vancouver, mas para fixar as ideias, lembremos a regra: sempre que você decide fazer um mulligan, embaralha sua mão de volta no deck e retira o mesmo número de cartas menos uma. Você pode repetir o processo quantas vezes quiser até não ter mais cartas e, no final, ganha um scry 1 de troco.

Foi anunciado no dia 26/02/2019, através de um artigo no site da Wizards, que será testada uma nova regra de mulligan no Mythic Championship (ProTour) de Londres, que será no formato Moderno e ocorrerá entre os dias 26 e 28 de abril de 2019, daí ser denominada mulligan de Londres. É razoável supor que a mudança já foi testada à exaustão internamente pelo fabricante, o que significa que deve haver poucas chances de que a nova regra não vingue. A nova regra é: sempre que você decide fazer o mulligan, embaralha sua mão de volta no deck, retira exatamente 7 cartas e então devolve para o fundo um número de cartas igual ao número de mulligans feitos até ali. Nada de scry pra você. O resultado é que, embora o mulligan vá te deixar com o mesmo número de cartas na mão inicial com relação à regra anterior, o número de cartas visto por você antes do keep é maior, o que deve fazer com que mulligans sejam menos punitivos. Verificar se isto procede ou não, na ponta do lápis, é um dos objetivos deste texto.

5. A MATEMÁTICA DO MULLIGAN

Mulligan de Vancouver (atual)

Para começar a atacar o problema do mulligan, precisamos saber as probabilidades de que uma determinada carta apareça numa mão de k cartas, para k de 1 a 7. Chamemos isto de P[k]. Vamos supor, por hora, que temos 4 cópias da carta. A correção para as outras multiplicidades é direta, bastando modificar o valor da entrada “Number of successes in sample” na calculadora hipergeométrica. Já conhecemos o resultado para k=7. Calcule para os demais valores. Para tanto, rode a calculadora com os mesmos dados mostrados anteriormente modificando apenas a entrada “Sample size”. Os resultados são: P[7] = 0,3995, P[6] = 0,3514, P[5] = 0,3006, P[4] = 0,2468, P[3] = 0,1899, P[2] = 0,1299, P[1] = 0,0667.

A complicação aqui é que encontrar uma determinada carta numa mão de 6 não é um problema equivalente a encontrar a carta quando você está disposto a “muligar” até 6 se for necessário. Evidentemente, a probabilidade de encontrar a carta numa mão de 6 é menor que numa mão de 7. No entanto, a de encontra-la quando há a predisposição para ir até 6 se necessário é maior que a de encontra-la numa mão de 7. Como computar isso?

Chamemos de P’[k] a probabilidade de encontrar ao menos uma cópia de algo específico quando se está disposto fazer mulligan até uma mão de k cartas. Já sabemos P’[7], que é igual a P[7] (zero mulligans). Para P’[6] precisamos SOMAR P’[7] com a probabilidade de que a carta NÃO esteja na mão de 7 cartas E, ao mesmo tempo, esteja na mão de 6. Para isto, lembremos a regra da intersecção, ou regra do “E”: a probabilidade de que dois eventos independentes ocorram simultaneamente é o PRODUTO das probabilidades individuais dos dois. Lembre também que a probabilidade de que algo NÃO ocorra é um menos a probabilidade de que ocorra (1-P). Assim:

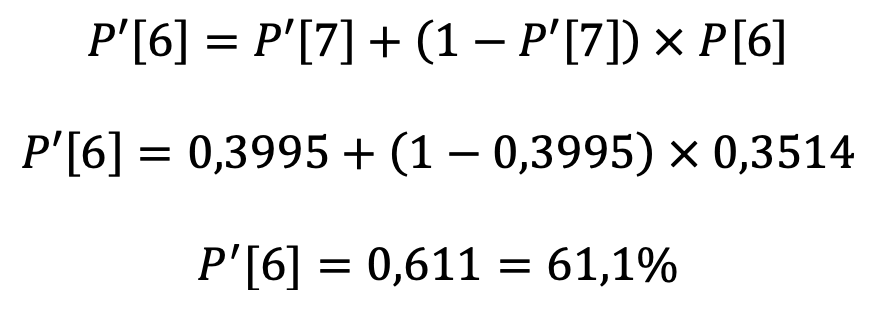
Generalizando, a probabilidade de encontrar ao menos uma cópia de uma carta específica quando se está disposto a fazer mulligan até k cartas é a probabilidade de encontra-la num mulligan até k+1 somada com a probabilidade de NÃO encontra-la até k+1 MULTIPLICADA pela de encontra-la na mão de k cartas. Simbolicamente:

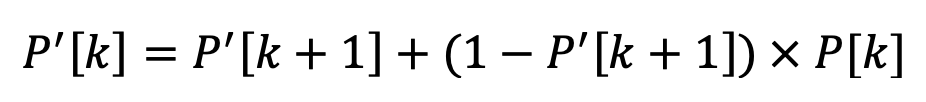
Apresentarei os resultados dos cálculos para todos os mulligans de uma forma mais palatável na seção 6. Só um minutinho que chegaremos lá.

Mulligan de Londres (novo)

O raciocínio envolvido no cálculo é essencialmente o mesmo, de modo que a última expressão continua válida. A diferença está nos valores de P[k] (“sem linha”). Note que, na regra nova, o custo do mulligan (uma carta a menos) é pago a posteriori, de modo que todas as mãos são mãos de 7 cartas para fins de cálculo. Isto é, os valores de P[k] são independentes de k e são sempre iguais a P[7]=0,3995.

Como exemplo, façamos o cálculo para a predisposição de realizar o mulligan até 6 com o novo formato (compare com o cálculo anterior e repare no que mudou):

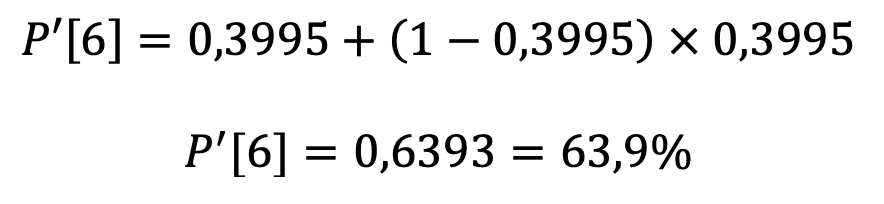
Não parece que o resultado mudou tanto assim, não é mesmo? Calma. Aguarde até você ver o que acontece nos mulligans para 5 cartas ou menos. Vamos aos resultados.

6. O MULLIGAN EM NÚMEROS

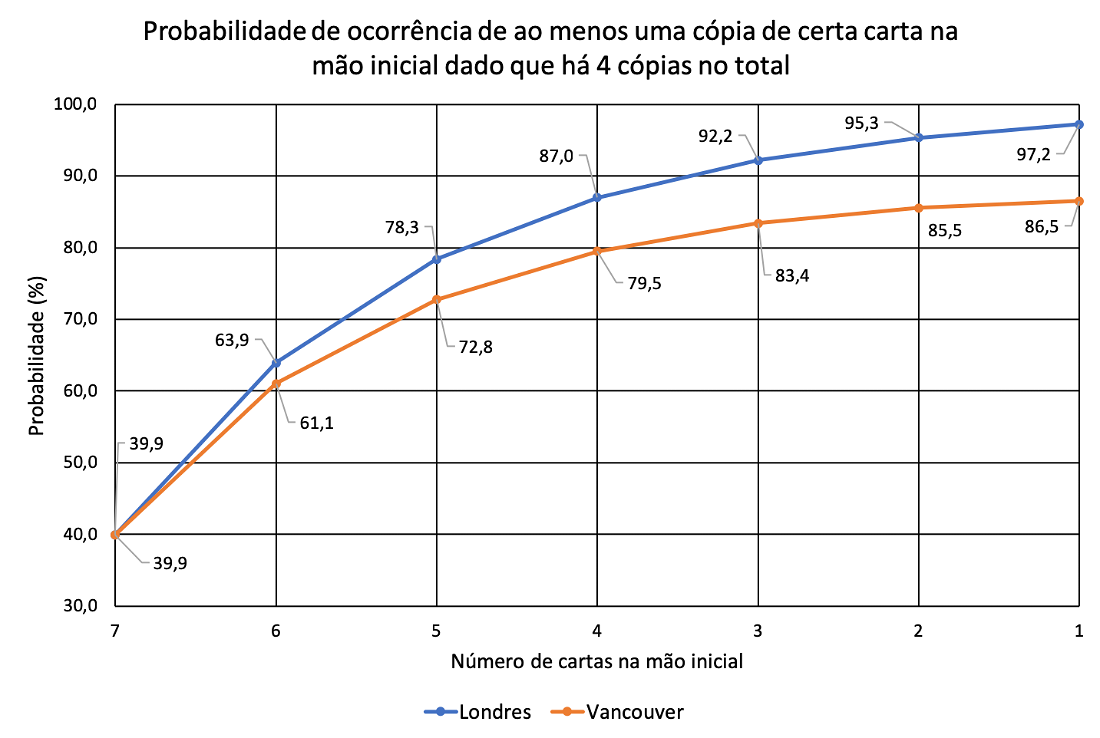
O gráfico abaixo mostra as probabilidades de se encontrar, na mão inicial, ao menos uma cópia de uma certa carta, cujo número total de cópias é 4, em função do número de cartas até o qual existe predisposição para fazer o mulligan.

O que a observação do gráfico mostra é que a mudança para o mulligan de Londres não altera significativamente as probabilidades com relação ao de Vancouver se você só estiver disposto a ir até seis cartas. Por outro lado, se você estiver propenso a mulligans mais agressivos a até cinco ou quatro cartas (ou menos) a diferença nas probabilidades é bastante sensível e favorável à regra nova.

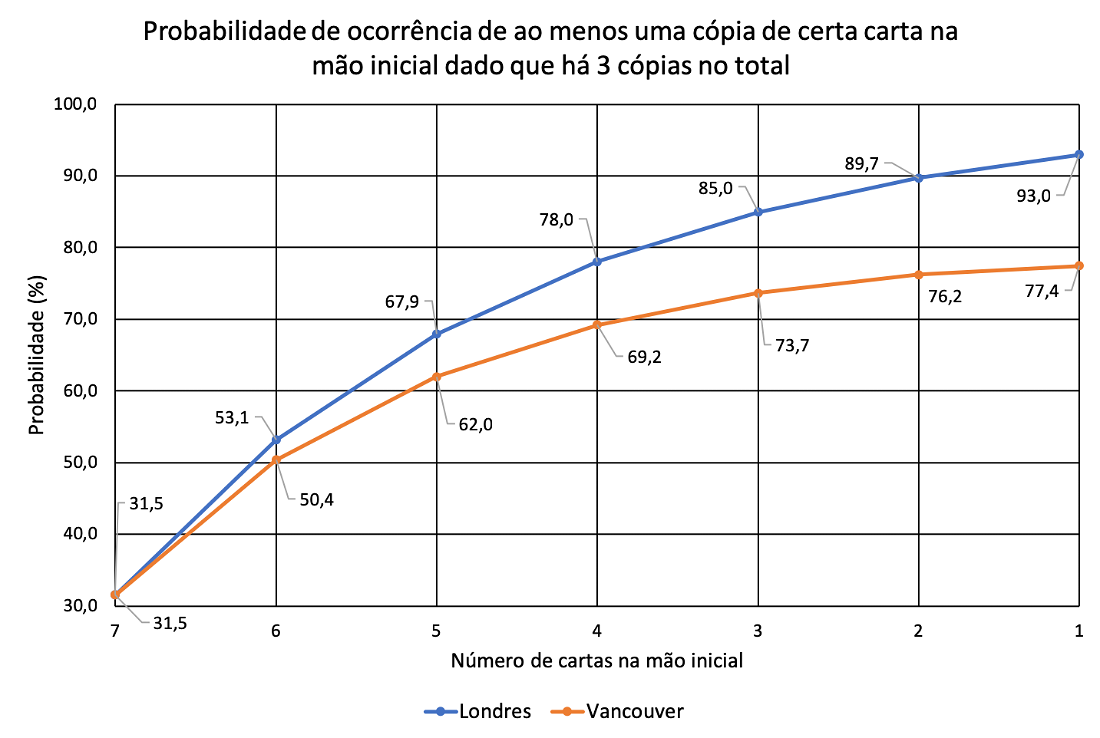
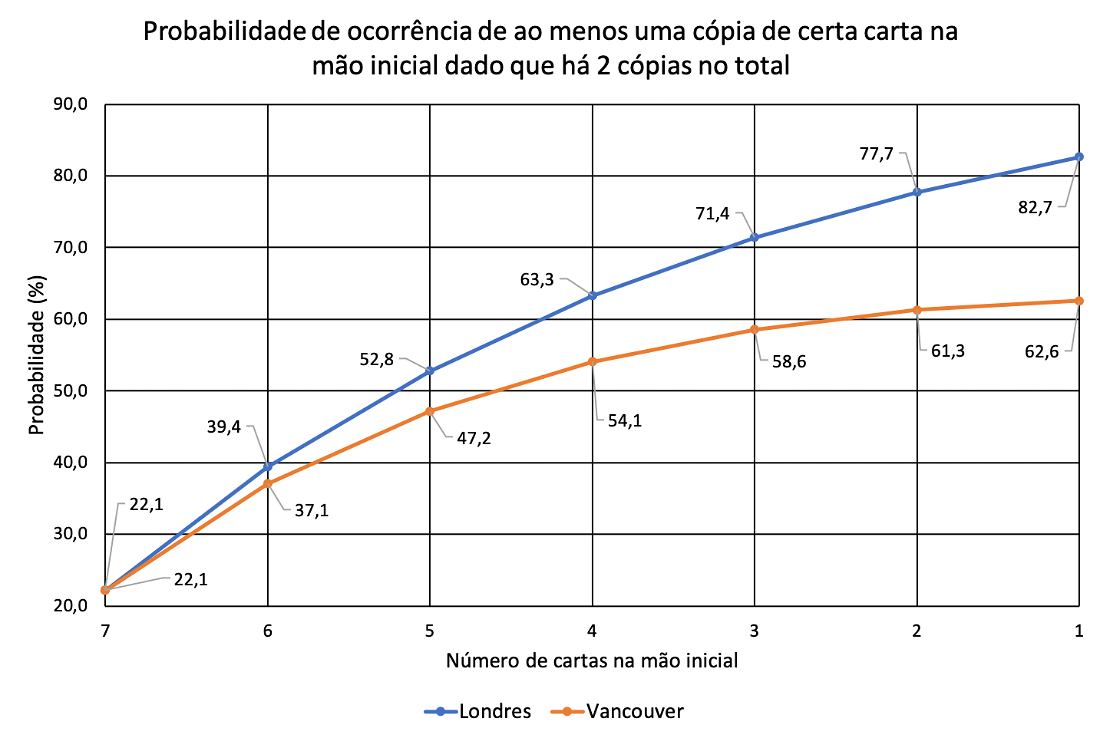
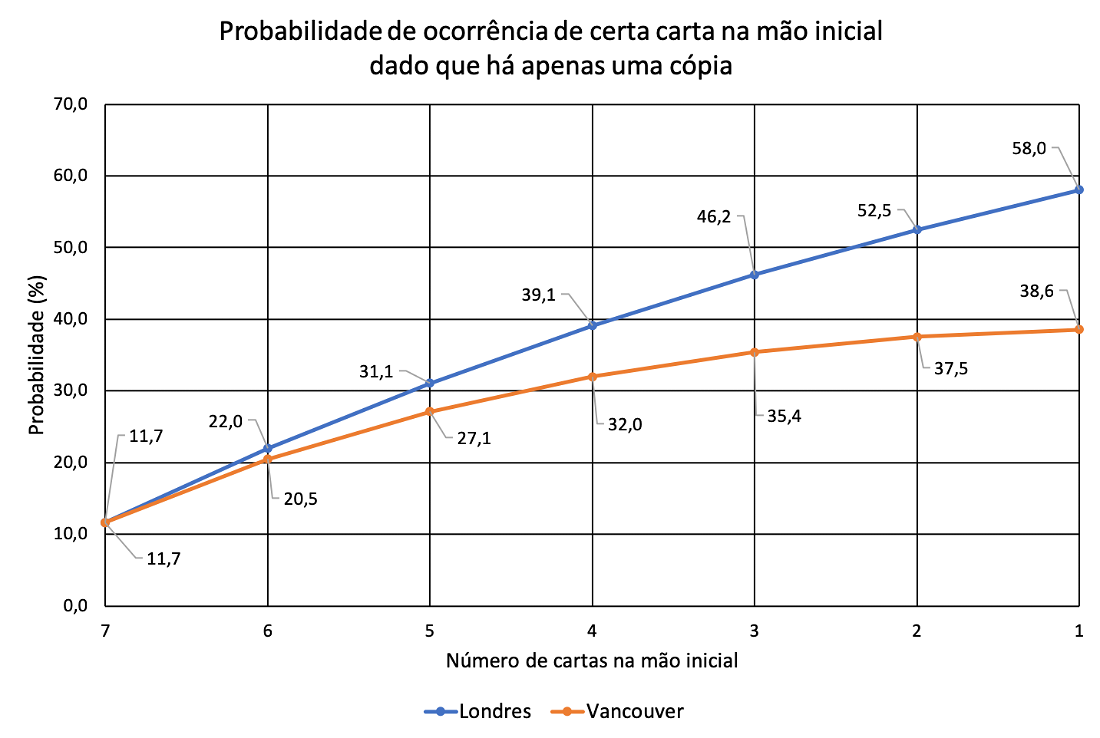
A seguir apresento, a título de curiosidade e base para possível referência, os resultados para os casos de cartas com três, duas ou apenas uma cópia no total.

7. CONCLUSÃO

Não há dúvidas de que o mulligan de Londres é uma modificação relevante no Magic, que merece nossa atenção e uma pitada de preocupação. Os números mostram que mulligans para cinco ou quatro cartas (ou menos) devem ser de fato menos punitivos com a regra nova na medida em que a probabilidade de encontrar peças específicas aumenta sensivelmente. O efeito esperado pela Wizards parece ser uma redução na incidência de games sem sentido, games em que alguém não consegue jogar Magic ao ser punido por um keep arriscado (terreno único, terrenos demais, lado errado da curva de mana, etc). Isso é especialmente importante num momento em que o fabricante investe pesado em e-sports. Este é um mercado no qual a empresa havia sido deixada para trás há bastante tempo, mas parece ter ganho uma boa dose de fôlego recentemente com o sucesso da nova plataforma online. Transmitir jogos em que a magia não acontece por causa da variância, seja no streaming do papel, do MOL ou do Arena, é péssima propaganda para potenciais novos jogadores. O novo mulligan pode ser uma resposta inteligente a esta pressão de mercado. Além disso, admita, você vai zicar menos mana e vai voltar pra casa do FNM mais feliz por isso.

O que esperar do efeito da mudança em formatos com raw power mais elevado que o T2, como o Moderno? Esta é uma pergunta que ninguém sabe responder com precisão agora. Vai favorecer decks de combo ou que dependem de peças específicas? No game 1, com certeza. Nos games 2 e 3, divirta-se tentando usar o cemitério com a linha preta em jogo, queimar alguém com a branca do outro lado, fazer o Karn na 3 tomando uma esfera do amortecimento quase certa na 2, etc. É, mas eu vou subir anti-hate pro seu hate. Claro, amigo, e isto é um raciocínio em espiral que não leva a lugar algum. Não me arrisco a especular mais do que isso sem a prática. Faremos todos o teste em breve muito provavelmente. Não será no GP ainda, não esqueça que o Magic Fest São Paulo acontece duas semanas antes do evento em Londres. O que me parece seguro afirmar agora é que as cartas de hate do sideboard serão mais importantes do que já são hoje no Moderno e que provavelmente algumas escolhas de side precisarão ser revistas para uma perspectiva de mulligans mais frequentes e agressivos. Apertemos os cintos e aguardemos mais um mês para ver direitinho no que vai dar.